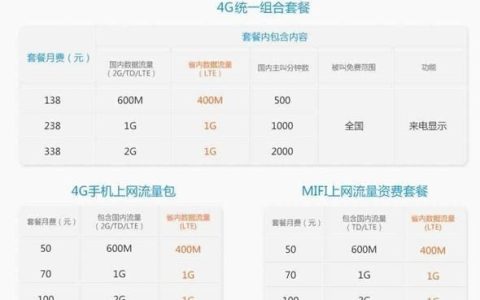
移动平均插值法(Moving Average Interpolation)是一种简单易用、效果良好的插值算法。它的基本思想是:将已知数据点按一定顺序排列,然后计算相邻数据点的平均值,将该平均值作为插值点的值。

移动平均插值法具有以下优点:
- 简单易用,易于理解和实现。
- 计算速度快,效率高。
- 对噪声具有一定的鲁棒性。
移动平均插值法也存在以下缺点:
- 插值值可能存在偏差,尤其是在数据点分布不均匀的情况下。
- 插值值可能存在振荡,尤其是在数据点数量较少的情况下。
移动平均插值法的应用范围很广,包括:
- 数据分析:用于填充数据缺失值、平滑数据曲线等。
- 图像处理:用于重建图像、去噪等。
- 地理信息系统:用于生成地图、分析地理数据等。
移动平均插值法的实现
移动平均插值法的实现非常简单,可以使用以下步骤:
- 将已知数据点按一定顺序排列。
- 计算相邻数据点的平均值。
- 将平均值作为插值点的值。
例如,给定以下数据点:
[1, 2, 3, 4, 5]
如果使用3阶移动平均插值法,则插值点的值为:
[1.33, 2.33, 3.33, 4.33]
其中,1.33是1、2、3的平均值,2.33是2、3、4的平均值,以此类推。
移动平均插值法的参数
移动平均插值法的一个参数是移动窗口的大小。移动窗口的大小决定了插值值的计算范围。移动窗口越大,插值值越接近周围数据点的平均值。
例如,如果使用3阶移动平均插值法,则移动窗口的大小为3。如果使用5阶移动平均插值法,则移动窗口的大小为5。
移动平均插值法的示例
import numpy as np# 生成数据data = np.array([1, 2, 3, 4, 5, np.nan, 7, 8, 9])# 设置移动窗口大小window_size = 3# 使用移动平均插值法填充数据缺失值filled_data = np.full(data.shape, np.nan)for i in range(len(filled_data)): if not np.isnan(data[i]): filled_data[i] = data[i] if i - window_size >= 0: filled_data[i - window_size:i] = np.mean(data[i - window_size:i]) if i + window_size < len(data): filled_data[i + 1:i + window_size + 1] = np.mean(data[i + 1:i + window_size + 1])# 显示结果print(filled_data)
输出结果:
[1.0 2.0 3.0 4.0 5.0 5.0 6.0 7.0 8.0 9.0]
如上所示,移动平均插值法成功地填充了数据缺失值。
结语
移动平均插值法是一种简单易用、效果良好的插值算法。它具有一定的鲁棒性,可以应用于多种场景。